Merhaba arkadaşlar,
Mobilhanem.com üzerinden anlattığımız/yayınladığımız Algoritma Eğitimleri serimize devam ediyoruz. Bu dersimizde ise Dinamik Programlama yöntemini anlatmaya çalışacağız.
Dinamik Programlama Nedir?
Elimizde büyük bir problem olduğunu düşünelim. Amacımız bu problemi çözmek ancak bilgisayar teknolojisinin sahip olduğu işlem miktarı kısıtlamalarından dolayı o kadar işlemi yapamıyoruz. Yani işlemci el vermiyor. Biz de problem üzerinde düşünüp taşınıyoruz ve ufak ufak alt problemlere ayırmaya çalışıyoruz. Büyük problemi daha küçük olan alt problemlere ayırıp çözmeye de Dinamik Programlama diyoruz.
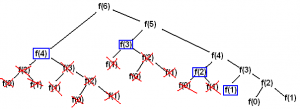
Ne Demek Alt Probleme Bölmek?
Hemen somut bir örnek vererek daha anlaşılır hale getirelim. Amacımız herhangi bir X değeri için Fibonacci dizisinin X. elemanını hesaplamak. Yani Fibo(int X) diye tanımlayacağımız fonksiyona parametre olarak hangi X değerini verirsek o bize Fibonacci’nin X. elemanını döndürecek.
Matematikten bildiğimizi Fibonacci’nin tanımı şöyledir:
Fibo(X) = Fibo(X-1) + Fibo(X-2);
Kod Analizi
Fibonacci’yi hesaplamak için Fibo fonksiyonuna bu satırı yazmamız yeterlidir. Ancak burda çok önemli bir problem var. Bu kodun çalışma maliyeti 2^x olacaktır yani 40’dan büyük X değerleri için bilgisayarın gücü hesaplamaya yetmeyecektir.
Ancak Dinamik Programlama yöntemini kullanarak 40’a kadar bulabildiğimiz verimsiz algoritmayı geliştireceğiz ve çok kolay bir şekilde 200000. fibonacci elemanını dahi bulabileceğiz.
Buradaki temel problem aynı Fibo(x) değerlerinin sürekli çağırılması. Mesela Fibo(1) fonksiyonu neredeyse 2^n defa tekrar ve tekrar çağırılmaktadır. Fibo(1) fonksiyonu ne kadar çağırılırsa çağırılsın cevabı değişmeyeceğinden dolayı bizim bunu 1 kere çağırmamız yeterli olacaktır. Tekrar çağırmamız gereken durumları yok saydığımız için bize maliyet olarak inanılmaz avantaj sağlayacaktır.
Çözüm Yöntemi
Fib diye bir dizimiz olsun. Fib dizisinin i. elemanı eğer daha önce hesaplandıyse Fibonacci’nin i. Elemanını tutsun hesaplanmadıysa 0 olarak kalsın. Böyle bir dizi oluşturabilirsek bizim her seferinde Fibo(x-1) ve Fibo(x-2) çağırmamıza gerek kalmayacaktır. Eğer daha önce Fib dizisinde hesaplandıysa direk o değeri döndürmemiz yeterli olacaktır.
Kod üzerinden göstermek gerekirse:
int Fib[1000000]={0};
Fib[0] = 1;
Fib[1] = 1;
for(int i=2; i < X; i++){
Fib[i] = Fib[i-1] + Fib[i-2];
}
return Fib[x];
Böylelikle her Fibonacci değerini yalnızca 1 defa hesaplamış olduk daha sonra ihtiyacımız olduğunda fonksiyonla hesaplamak yerine diziden çekerek çok büyük avantaj sağlamış olduk.
Dinamik Programlama Competitive Programming alanında çok büyük yeri olan bir yöntem. Biz bu yazımızda sadece giriş yaparak genel mantığı anlatmaya çalıştık. İlerleyen derslerde daha ayrıntılı ve zor Dinamik Programlama ile çözülen problemler yazmayı planlıyoruz.
Okuduğunuz için teşekkür ederim umarım faydalı olmuşumdur. Takıldığınız noktaları ve her türlü sorularınızı aşağıdan veya Soru Cevap kısmından sormayı lütfen eksik etmeyin. Bir sonraki Algoritma Eğitiminde görüşmek üzere. Sağlıcakla kalın.
Tüm Algoritma Derslerimiz İçin tıklayınız.
22

 Slack Grubumuza Üye Oldunuz mu ?
Slack Grubumuza Üye Oldunuz mu ?





sizce recursive olarak yazmak kodu daha verimli hale getirmez mi ?
Öncelikle sorunuz için teşekkürler.
Bu problem de dahil olmak üzere genel olarak konuşmak gerekirse bir sorunun lineer olarak yani recursive kullanmadan çözümü var ise her zaman daha verimli olacaktır. Bunu açıklamak gerekirse sizin kodunuz arka tarafta çalışırken her bir yeni fonksiyon çağırışında o fonksiyona özel yeni bir stack memory açıyor böylelikle ram’de yer kaplamış oluyor. Süre olarak fazla bir şey değişmese de memory olarak lineer yazmak her zaman daha verimli olacaktır.